Progressões Aritméticas e Geométricas: Conceitos e Aplicações

Introdução

As progressões aritméticas (P.A.) e as progressões geométricas (P.G.) são sequências numéricas amplamente utilizadas em matemática para descrever fenômenos que apresentam padrões regulares de crescimento ou diminuição. Elas têm aplicações práticas em áreas como economia, física, biologia e até no cotidiano. Neste resumo, discutiremos os conceitos fundamentais de progressões aritméticas e geométricas, suas fórmulas, exemplos práticos e a importância dessas sequências no dia a dia.

Progressões Aritméticas (P.A.)

O que é uma Progressão Aritmética?

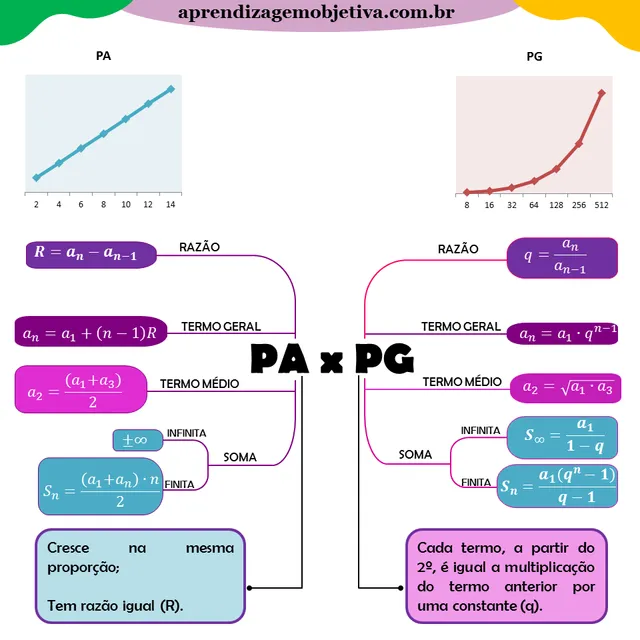
Uma progressão aritmética é uma sequência de números em que a diferença entre dois termos consecutivos é sempre a mesma. Essa diferença constante é chamada de razão da progressão e é representada por \( r \).

A fórmula geral para a enésima posição de uma progressão aritmética é:

a_n = a_1 + (n - 1) \cdot r

Onde:

• a_n é o n-ésimo termo da sequência,
• a_1 é o primeiro termo da sequência,
• r é a razão da progressão (a diferença entre dois termos consecutivos),
• n é o número do termo que queremos calcular.

Exemplo de Progressão Aritmética

Considere a sequência \( 2, 5, 8, 11, 14, \dots \), em que a razão \( r = 3 \). Podemos usar a fórmula para encontrar qualquer termo dessa progressão.

Se quisermos encontrar o 5º termo (\( a_5 \)), aplicamos a fórmula:

a_5 = 2 + (5 - 1) \cdot 3 = 2 + 12 = 14

Logo, o 5º termo da sequência é 14.

Aplicações de Progressões Aritméticas

As progressões aritméticas são usadas para modelar situações de crescimento ou diminuição constante, como:

• Sistemas de pagamento parcelado: onde cada pagamento tem o mesmo valor (por exemplo, o valor das parcelas de um financiamento).
• Crescimento de salários: quando há aumentos periódicos fixos no salário.
• Distâncias percorridas: como o deslocamento de um carro a uma velocidade constante.

Progressões Geométricas (P.G.)

O que é uma Progressão Geométrica?

Uma progressão geométrica é uma sequência em que cada termo após o primeiro é obtido multiplicando o termo anterior por uma constante chamada razão da progressão, representada por \( q \).

A fórmula geral para o enésimo termo de uma progressão geométrica é:

a_n = a_1 \cdot q^{n - 1}

Onde:

• a_n é o n-ésimo termo da sequência,
• a_1 é o primeiro termo da sequência,
• q é a razão da progressão (o fator pelo qual cada termo é multiplicado para gerar o próximo),
• n é o número do termo que queremos calcular.

Exemplo de Progressão Geométrica

Considere a sequência \( 3, 6, 12, 24, 48, \dots \), em que a razão \( q = 2 \). Podemos usar a fórmula para encontrar qualquer termo dessa progressão.

Se quisermos encontrar o 5º termo (\( a_5 \)), aplicamos a fórmula:

a_5 = 3 \cdot 2^{5 - 1} = 3 \cdot 16 = 48

Logo, o 5º termo da sequência é 48.

Aplicações de Progressões Geométricas

As progressões geométricas são amplamente aplicadas em cenários que envolvem crescimento ou decrescimento exponencial, como:

• Cálculos de juros compostos: onde o valor do capital cresce multiplicado por uma taxa de juros a cada período.
• Crescimento populacional: quando a população de uma espécie se multiplica de forma constante.
• Radioatividade: a decaída de elementos radioativos segue uma progressão geométrica, pois a quantidade de radiação diminui a uma taxa constante.

Fórmulas Relevantes

Progressão Aritmética (P.A.)

• Fórmula do enésimo termo:

  a_n = a_1 + (n - 1) \cdot r

• Soma dos primeiros \( n \) termos:

  S_n = (n / 2) \cdot (a_1 + a_n)

Progressão Geométrica (P.G.)

• Fórmula do enésimo termo:

  a_n = a_1 \cdot q^{n - 1}

• Soma dos primeiros \( n \) termos (quando \( q \neq 1 \)):

  S_n = a_1 \cdot \frac{1 - q^n}{1 - q}

Conclusão

As progressões aritméticas e geométricas são conceitos fundamentais dentro da matemática, com ampla aplicação em diversas áreas do conhecimento e no cotidiano. As P.A.s são usadas para modelar situações com crescimento ou diminuição constante, como no caso de pagamentos parcelados ou aumentos salariais. Já as P.G.s são essenciais para entender processos de crescimento ou decaimento exponenciais, como nos cálculos de juros compostos e no crescimento populacional.

Compreender essas sequências e suas fórmulas é fundamental para resolver problemas do dia a dia, seja no planejamento financeiro, no estudo da física ou até mesmo na análise de dados e tendências. O domínio das progressões é uma habilidade importante não apenas em contextos acadêmicos, mas também em situações práticas, como finanças pessoais e cálculos de investimentos.