Oscilações e Vibrações de Corpos: Entendendo o Movimento Harmônico

Introdução

As oscilações e vibrações de corpos são fenômenos físicos fundamentais que ocorrem quando um sistema se move de maneira repetitiva ao redor de uma posição de equilíbrio. Esses movimentos estão presentes em diversos contextos da nossa vida cotidiana, desde os movimentos de pêndulos até as vibrações das cordas de um violão. O estudo das oscilações e vibrações é essencial para entender muitos conceitos da física e suas aplicações tecnológicas, como em motores, sistemas de som e até mesmo na engenharia sísmica. Este artigo tem como objetivo explicar o que são as oscilações e vibrações, as características que definem esses movimentos e alguns exemplos práticos.

1. O que são Oscilações e Vibrações?

As oscilações e vibrações podem ser definidas como movimentos que se repetem no tempo. Eles ocorrem quando um corpo se desloca de uma posição de equilíbrio, volta para ela e repete esse movimento de forma regular. Esses movimentos podem ser classificados em duas grandes categorias:

1.1. Oscilações

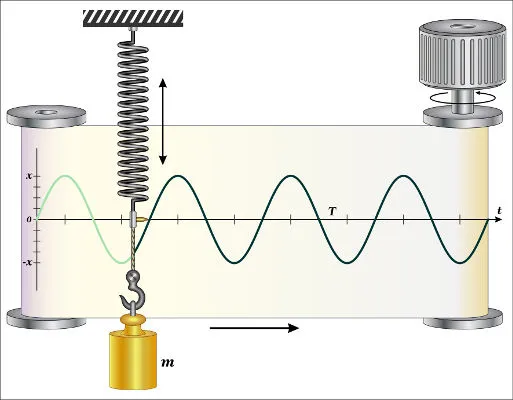
Uma oscilação é um movimento periódico de um sistema em torno de uma posição de equilíbrio. Esse movimento pode ser descrito por parâmetros como a amplitude (máxima distância do ponto de equilíbrio), a frequência (quantas oscilações ocorrem por unidade de tempo) e o período (tempo necessário para realizar uma oscilação completa).

1.2. Vibrações

As vibrações são oscilações de um objeto em torno de uma posição de equilíbrio, mas com frequências que podem variar e com amplitudes que podem ser pequenas, como as vibrações de uma corda de violão ou a vibração de um celular em modo silencioso. Elas são geralmente descritas em termos de movimento elástico, onde forças de restauração (como a tensão ou a compressão) atuam para trazer o corpo de volta à posição de equilíbrio.

2. Movimento Harmônico Simples (MHS)

O movimento harmônico simples (MHS) é um tipo de oscilação idealizada, onde a força restauradora que age sobre o corpo é diretamente proporcional à sua deslocação da posição de equilíbrio. Isso resulta em um movimento regular e previsível, com uma amplitude constante.

2.1. Lei de Hooke

O MHS é frequentemente associado à Lei de Hooke, que descreve o comportamento elástico de materiais. De acordo com a Lei de Hooke, a força restauradora que age sobre um objeto elástico (como uma mola) é proporcional ao deslocamento desse objeto em relação à sua posição de equilíbrio:

F = -k · x

Onde:

• F é a força restauradora,
• k é a constante elástica (rigidez da mola),
• x é o deslocamento da posição de equilíbrio.

A força é negativa porque age na direção oposta ao deslocamento, tentando restaurar o objeto à sua posição de equilíbrio.

2.2. Equação do Movimento Harmônico Simples

A equação para a posição de um objeto em movimento harmônico simples é dada por:

x(t) = A · cos(ω t + φ)

Onde:

• x(t) é a posição do objeto em função do tempo,
• A é a amplitude (máxima distância do ponto de equilíbrio),
• ω é a frequência angular (ω = 2π f),
• f é a frequência (número de oscilações por segundo),
• φ é a fase inicial.

3. Período e Frequência de Oscilações

O período (T) de uma oscilação é o tempo necessário para que o objeto complete um ciclo completo de movimento, ou seja, para voltar à sua posição inicial. Já a frequência (f) é o número de ciclos que ocorrem em uma unidade de tempo. Eles estão relacionados pela fórmula:

f = 1 / T

3.1. Movimento de Pêndulo

Um exemplo clássico de oscilação é o movimento de um pêndulo simples. Um pêndulo consiste em um fio leve e inextensível, com uma massa (ou “bob”) na extremidade, que oscila para frente e para trás devido à força gravitacional.

Para um pêndulo simples de pequena amplitude, o período de oscilação é dado por:

T = 2π · √(L / g)

Onde:

• T é o período,
• L é o comprimento do fio,
• g é a aceleração da gravidade.

Esse movimento é aproximadamente harmônico para pequenas amplitudes de oscilação, o que significa que ele pode ser descrito por uma equação do tipo x(t) = A · cos(ω t + φ).

4. Exemplos Práticos de Oscilações e Vibrações

As oscilações e vibrações estão presentes em muitos aspectos do nosso cotidiano e na tecnologia moderna:

4.1. Vibração de Cordas

Em instrumentos musicais como o violão, a vibração das cordas é responsável pela produção do som. Quando a corda é pressionada e puxada, ela oscila de acordo com a sua frequência natural, gerando ondas sonoras. A frequência de vibração da corda depende do seu comprimento, da tensão e da sua densidade.

4.2. Motores Elétricos

Os motores elétricos frequentemente utilizam a ideia de vibrações e oscilações para gerar movimento. No caso dos motores de corrente contínua (CC), a rotação do motor pode ser descrita como uma série de oscilações. A interação entre o campo magnético e a corrente elétrica no motor causa a oscilação do rotor, convertendo a energia elétrica em energia mecânica.

4.3. Vibrações em Edifícios e Estruturas

Em grandes edifícios e pontes, as vibrações podem ser tanto um problema quanto uma ferramenta útil. A engenharia civil utiliza o estudo das vibrações para projetar edifícios que resistam a terremotos e outras forças externas. Equipamentos de controle de vibrações, como amortecedores, são usados para reduzir os efeitos das vibrações.

5. Conclusão

As oscilações e vibrações de corpos são fundamentais para entender muitos aspectos da física e têm aplicações práticas importantes na engenharia, música e outras áreas. O movimento harmônico simples é um modelo que ajuda a descrever muitos desses movimentos, enquanto a relação entre frequência, amplitude e período é essencial para compreender como os sistemas oscilantes funcionam. O estudo dessas propriedades é crucial para a construção de dispositivos tecnológicos e para o desenvolvimento de novas tecnologias.

Referências

• HALLIDAY, D.; RESNICK, R.; WALKER, J. Fundamentos de Física. 10ª ed. Rio de Janeiro: LTC, 2011.
• SERWAY, R. A.; JEWETT, J. W. Física para Cientistas e Engenheiros. 9ª ed. São Paulo: