Frações: Conceito, Tipos e Operações
As frações são uma das formas fundamentais de representação de números na matemática, sendo uma maneira de expressar uma parte de um todo. Elas são utilizadas para descrever divisões e compartilhamentos, sendo uma ferramenta essencial não só na matemática, mas também em situações cotidianas, como medir ingredientes em uma receita ou dividir algo entre várias pessoas. Neste artigo, exploraremos os conceitos principais das frações, seus tipos, operações e a importância delas no nosso dia a dia.
O que são Frações?
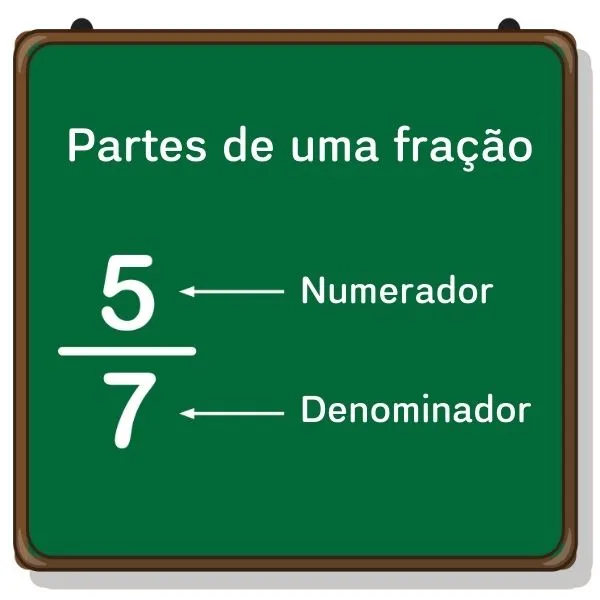
Uma fração é representada por dois números inteiros: o numerador (o número acima da linha de fração) e o denominador (o número abaixo da linha de fração). O numerador indica quantas partes estamos considerando, enquanto o denominador indica o número total de partes em que o todo foi dividido.
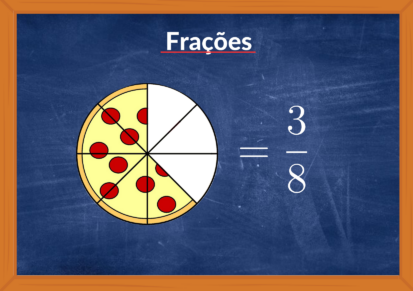
Exemplo: Se dividirmos uma pizza em 8 partes iguais e comermos 3 fatias, podemos representar isso como a fração 3/8. Aqui, 3 é o numerador (as fatias que comemos) e 8 é o denominador (o total de fatias da pizza).
É importante lembrar que o termo “numerador” refere-se ao número de partes que estamos considerando e o “denominador” ao número total de partes do inteiro.
Tipos de Frações
As frações podem ser classificadas em diferentes tipos, de acordo com as relações entre numerador e denominador. Vejamos os principais tipos:
1. Fração Própria
São frações em que o numerador é menor que o denominador, representando um número menor que 1.
Exemplo: 3/5 Aqui, o numerador (3) é menor que o denominador (5), o que indica que a fração é menor que 1.
2. Fração Imprópria
São frações em que o numerador é maior que o denominador, representando um número maior que 1.
Exemplo: 7/4 Neste caso, o numerador (7) é maior que o denominador (4), indicando que a fração é maior que 1.
3. Fração Aparente
São frações em que o numerador é múltiplo do denominador. Esse tipo de fração é, na verdade, um número inteiro.
Exemplo: 6/3 = 2 A fração 6/3 é igual a 2, pois 6 é um múltiplo de 3.
4. Fração Mista
É formada por uma parte inteira e uma parte fracionária. Quando escrevemos frações mistas, o número inteiro é combinado com uma fração própria.
Exemplo: 1 2/5 Neste caso, temos um inteiro (1) e uma fração própria (2/5), formando uma fração mista.
Outros Tipos de Frações:
Além das frações mencionadas, há outras classificações, como frações equivalentes, irredutíveis, unitárias, egípcias, decimais, compostas, contínuas e algébricas. Cada uma dessas frações possui características específicas e é utilizada em contextos variados dentro da matemática e de outras áreas do conhecimento.
Operações com Frações
As frações podem ser somadas, subtraídas, multiplicadas e divididas. As regras para cada operação dependem dos denominadores das frações envolvidas.
1. Adição de Frações
Quando somamos frações, devemos verificar se os denominadores são iguais ou diferentes:
- Se os denominadores forem iguais: basta somar os numeradores e manter o denominador.
- Se os denominadores forem diferentes: devemos encontrar o Mínimo Múltiplo Comum (MMC) entre os denominadores e ajustar as frações para que tenham denominadores iguais. Após isso, somamos os numeradores.
Exemplo:
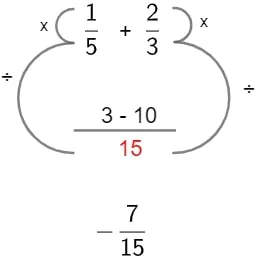
1/5 + 2/3 O MMC de 5 e 3 é 15. Então, as frações se tornam 3/15 e 10/15. Somando os numeradores: 3 + 10 = 13, resultando em 13/15.
2. Subtração de Frações
A subtração de frações segue o mesmo raciocínio da adição. Se os denominadores forem iguais, subtraímos os numeradores e mantemos o denominador. Caso contrário, fazemos o MMC e depois subtraímos os numeradores.
Exemplo:
5/8 - 2/8 = 3/8
Exemplo:
3. Multiplicação de Frações
Para multiplicar frações, basta multiplicar os numeradores entre si e os denominadores entre si.
Exemplo:
2/3 × 4/5 = 8/15
4. Divisão de Frações
Na divisão de frações, multiplicamos a primeira fração pelo inverso da segunda. Ou seja, invertemos o numerador e o denominador da segunda fração e, em seguida, realizamos a multiplicação.
Exemplo:
2/3 ÷ 4/5 = 2/3 × 5/4 = 10/12 = 5/6
Simplificação de Frações
A simplificação de frações consiste em reduzir uma fração para sua forma mais simples, ou seja, em que o numerador e o denominador não possuem mais divisores em comum, exceto o 1.
Exemplo: 12/18 pode ser simplificado dividindo o numerador e o denominador por 6, resultando em 2/3.
História das Frações
O conceito de fração remonta ao Antigo Egito, por volta de 3.000 a.C., quando os matemáticos egípcios começaram a utilizar frações para medir as terras. No entanto, as frações que eles usavam eram frações unitárias, ou seja, frações com numerador igual a 1. A palavra “fração” vem do latim fractio, que significa “partido”, refletindo a ideia de dividir um todo em partes.
No Egito Antigo, as frações eram utilizadas para dividir os terrenos agrícolas, especialmente para resolver problemas relacionados a inundações de rios, que alteravam os limites das propriedades.
Conclusão
As frações são um conceito fundamental em matemática, utilizadas para representar partes de um inteiro ou divisões entre quantidades. Elas são essenciais em muitas áreas do conhecimento, desde a matemática pura até aplicações práticas no cotidiano. Entender os diferentes tipos de frações e as operações com elas permite uma maior compreensão do mundo ao nosso redor e facilita a resolução de problemas de diversas naturezas.