Exercícios de Geometria: resolvidos e explicados

Exercício 1: Triângulo Retângulo – Teorema de Pitágoras
Enunciado:
Considere o triângulo retângulo mostrado abaixo. Sabemos que os catetos possuem medidas de 6 cm e 8 cm. Determine a medida da hipotenusa.
Imagem do Triângulo Retângulo
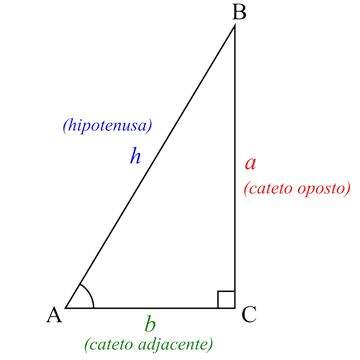
Resolução e Explicação:
Passo 1: O triângulo é retângulo, o que significa que ele possui um ângulo de 90 graus. Para encontrar a medida da hipotenusa, podemos aplicar o Teorema de Pitágoras.
Passo 2: O Teorema de Pitágoras diz que, em um triângulo retângulo, o quadrado da hipotenusa (a) é igual à soma dos quadrados dos catetos (b e c):
a² = b² + c²
Passo 3: Substituindo os valores dos catetos:
a² = 6² + 8² = 36 + 64 = 100
Passo 4: Agora, tiramos a raiz quadrada dos dois lados:
a = √100 = 10 cm
Portanto, a medida da hipotenusa é 10 cm.
Exercício 2: Perímetro de um Quadrado
Enunciado:
Calcule o perímetro de um quadrado cujo lado mede 7 cm.
Resolução e Explicação:
Passo 1: O perímetro de um quadrado é dado pela fórmula:
P = 4 × L
Onde L é a medida de um dos lados do quadrado.
Passo 2: Substituímos o valor do lado do quadrado:
P = 4 × 7 = 28 cm
Portanto, o perímetro do quadrado é 28 cm.
Exercício 3: Área de um Círculo
Enunciado:
Calcule a área de um círculo cujo raio é 5 cm. Utilize π ≈ 3,14.
Resolução e Explicação:
Passo 1: A fórmula da área do círculo é:
A = π × r²
Onde r é o raio do círculo.
Passo 2: Substituímos o valor do raio e de π:
A = 3,14 × 5² = 3,14 × 25 = 78,5 cm²
Portanto, a área do círculo é 78,5 cm².
Exercício 4: Volume de um Cubo
Enunciado:
Calcule o volume de um cubo cujo lado mede 4 cm.
Resolução e Explicação:
Passo 1: A fórmula do volume de um cubo é:
V = L³
Onde L é a medida de um dos lados do cubo.
Passo 2: Substituímos o valor do lado do cubo:
V = 4³ = 4 × 4 × 4 = 64 cm³
Portanto, o volume do cubo é 64 cm³.
Exercício 5: Área de um Triângulo
Enunciado:
Calcule a área de um triângulo cuja base mede 10 cm e a altura é de 6 cm.
Resolução e Explicação:
Passo 1: A fórmula da área de um triângulo é:
A = (b × h) / 2
Onde b é a base e h é a altura do triângulo.
Passo 2: Substituímos os valores da base e altura:
A = (10 × 6) / 2 = 60 / 2 = 30 cm²
Portanto, a área do triângulo é 30 cm².