Arranjo, Combinação e Permutação: Conceitos e Aplicações Práticas
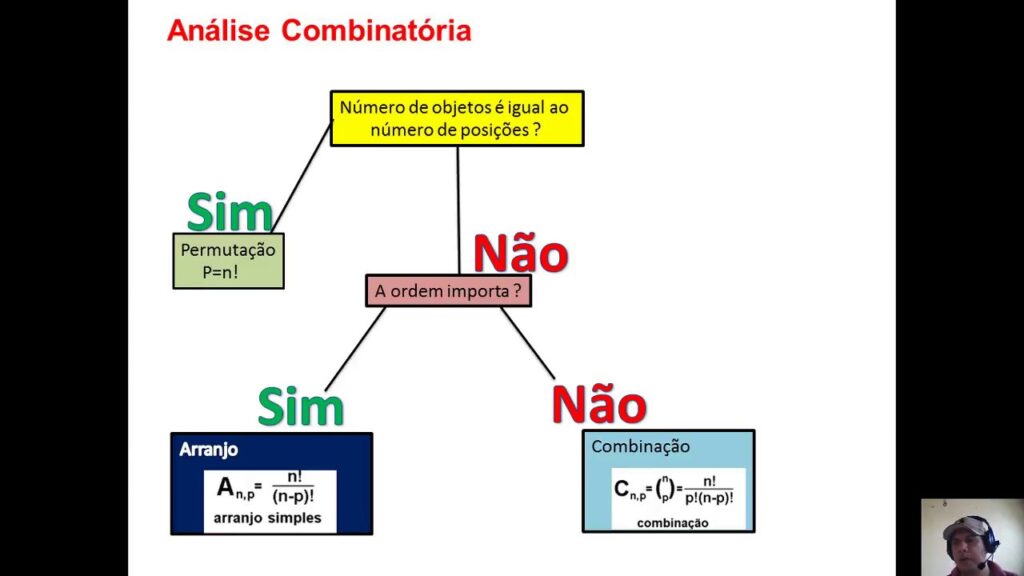
O estudo de arranjos, combinações e permutações pertence à área da Matemática conhecida como Combinatória, que lida com o número de maneiras diferentes de selecionar ou organizar elementos dentro de um conjunto, levando em consideração ou não a ordem desses elementos. Abaixo, apresento um resumo detalhado de cada um desses conceitos, com suas fórmulas e exemplos práticos de aplicação.
1. Permutação
Definição: Permutação refere-se à organização ou disposição de todos ou de alguns elementos de um conjunto, onde a ordem dos elementos é fundamental. Em uma permutação, estamos interessados em todas as possíveis maneiras de organizar os elementos, sem deixar nenhum de fora.
Fórmula: A fórmula para calcular o número de permutações de n elementos distintos, denotada por P(n), é dada por:
P(n) = n!
Onde n! (lê-se “n fatorial”) é o produto de todos os números inteiros de 1 até n. Ou seja, n! = n × (n-1) × (n-2) × ... × 1.
Se o problema envolver apenas a permutação de uma parte do conjunto, ou seja, permutação de r elementos de um total de n elementos, a fórmula é:
P(n, r) = n! / (n - r)!
Exemplo de Aplicação: Em uma corrida com 5 atletas, quantas formas diferentes de organizar a chegada dos atletas existem? A resposta é dada por P(5) = 5! = 5 × 4 × 3 × 2 × 1 = 120. Logo, existem 120 maneiras diferentes de organizar a chegada dos atletas.
Cálculo da Permutação
Para 5 atletas, temos a permutação:
P(5) = 5! = 5 × 4 × 3 × 2 × 1 = 120
Portanto, existem 120 maneiras diferentes de organizar a chegada dos 5 atletas na corrida.
2. Arranjo
Definição: O arranjo é um tipo de permutação em que apenas uma parte dos elementos de um conjunto é organizada, mas, ao contrário das permutações gerais, não consideramos todos os elementos. Aqui, a ordem dos elementos também é importante, e estamos interessados nas possíveis organizações de r elementos selecionados de um conjunto de n elementos.
Fórmula: A fórmula para calcular o número de arranjos de r elementos de um conjunto de n elementos, denotada por A(n, r), é dada por:
A(n, r) = n! / (n - r)!
Exemplo de Aplicação: Em um jogo de bingo, há 30 bolas numeradas e precisamos sortear 5 bolas. Quantas maneiras diferentes podemos escolher 5 bolas e organizá-las? A resposta é dada por A(30, 5) = 30! / (30 - 5)! = 30! / 25!.
Cálculo do Arranjo
Para 30 bolas e sorteio de 5 bolas:
A(30, 5) = 30! / 25! = 30 × 29 × 28 × 27 × 26 = 14250600
Portanto, existem 14.250.600 maneiras diferentes de escolher e organizar as 5 bolas do sorteio.
3. Combinação
Definição: A combinação é um conceito em que a ordem dos elementos não importa. Ou seja, o foco está em selecionar os elementos de um conjunto, independentemente de sua disposição ou organização. Esse conceito é utilizado quando queremos saber quantas formas diferentes podemos escolher um subconjunto de elementos de um conjunto maior, sem nos preocuparmos com a ordem em que esses elementos são selecionados.
Fórmula: A fórmula para calcular o número de combinações de r elementos de um conjunto de n elementos, denotada por C(n, r), é dada por:
C(n, r) = n! / (r! (n - r)!)
Exemplo de Aplicação: Em um sorteio de 6 números de um total de 49 (como na loteria), quantas diferentes combinações de 6 números podem ser sorteadas? A resposta é dada por C(49, 6) = 49! / (6! (49 - 6)!).
Cálculo da Combinação
Para 49 números e sorteio de 6 números:
C(49, 6) = 49! / (6! × 43!) = 49 × 48 × 47 × 46 × 45 × 44 / (6 × 5 × 4 × 3 × 2 × 1) = 13983816
Portanto, existem 13.983.816 maneiras diferentes de selecionar 6 números para o sorteio.
4. Comparação entre Permutação, Arranjo e Combinação
| Conceito | Ordem importa? | Fórmula | Exemplo |
|---|---|---|---|
| Permutação | Sim | P(n) = n! ou P(n, r) = n! / (n - r)! | Organizar 5 atletas em uma corrida |
| Arranjo | Sim | A(n, r) = n! / (n - r)! | Selecionar e organizar 5 bolas em um sorteio de bingo |
| Combinação | Não | C(n, r) = n! / (r!(n - r)!) | Selecionar 6 números na loteria sem importar a ordem |
5. Importância e Aplicações Práticas
Esses conceitos têm várias aplicações práticas no cotidiano e em diversas áreas, como:
- Estatísticas e Probabilidades: Calcular as probabilidades de diferentes eventos ocorrerem, como em sorteios e loterias.
- Algoritmos Computacionais: Utilizados na criação de algoritmos para resolver problemas de otimização, como no planejamento de rotas, jogos e criptografia.
- Análise de Dados e Pesquisa: Cálculos de amostras e seleções de dados em pesquisas científicas ou estudos de mercado.
Em áreas como a biologia, combinatória pode ser usada para calcular as possibilidades de combinações genéticas, enquanto na administração, pode ajudar a determinar as melhores formas de organizar equipes ou recursos.
6. Conclusão
Os conceitos de arranjo, combinação e permutação são fundamentais na matemática, especialmente no campo da combinatória. Eles fornecem as ferramentas para entender como elementos podem ser organizados ou selecionados de um conjunto, considerando ou não a ordem. Cada um desses conceitos é aplicado de maneira distinta, dependendo da situação e do problema em questão. A compreensão desses conceitos é essencial não apenas para a resolução de problemas matemáticos, mas também para diversas aplicações práticas no cotidiano, desde jogos de azar até a análise de grandes volumes de dados.