Análise Combinatória: Como Calcular Probabilidades e Possibilidades
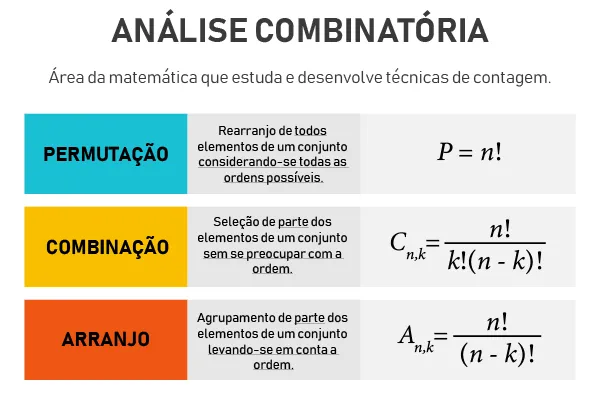
A Análise Combinatória é um ramo da matemática que lida com a contagem, a organização e a análise das diferentes maneiras em que os elementos de um conjunto podem ser dispostos, combinados ou escolhidos. Ela é fundamental para o cálculo de probabilidades, permitindo determinar a quantidade de possibilidades em determinados cenários e, a partir disso, calcular a probabilidade de eventos específicos ocorrerem.
Principais Conceitos da Análise Combinatória
1. Permutação
A permutação refere-se à disposição ordenada de todos ou alguns elementos de um conjunto. Quando consideramos todos os elementos de um conjunto, o número de permutações é dado por P(n, n), onde n é o número de elementos do conjunto.
Fórmula de permutação:
P(n, r) = n! / (n - r)!Onde:
né o número total de elementos;ré o número de elementos a serem escolhidos e ordenados;!é o fatorial de um número.
Exemplo: Se tivermos 3 livros e quisermos saber de quantas formas podemos ordená-los em uma estante, a permutação seria:
P(3, 3) = 3! / (3 - 3)! = 62. Combinação
A combinação é uma seleção de elementos sem considerar a ordem. Ou seja, a combinação é utilizada quando a ordem dos elementos não importa. A fórmula para calcular o número de combinações de r elementos escolhidos de um conjunto de n elementos é dada por:
C(n, r) = n! / (r! (n - r)!)Onde:
né o número total de elementos do conjunto;ré o número de elementos a serem escolhidos;!representa o fatorial.
Exemplo: Se temos 5 pessoas e queremos selecionar 2 para um cargo de comitê, sem importar a ordem, o número de combinações seria:
C(5, 2) = 5! / (2! (5 - 2)!) = 103. Princípio da Multiplicação
Este princípio afirma que, se uma tarefa pode ser realizada de m maneiras e uma segunda tarefa pode ser realizada de n maneiras, então as duas tarefas podem ser realizadas em m x n maneiras, ou seja, o número total de possibilidades é o produto das possibilidades de cada uma das tarefas.
Exemplo: Se um jogo de azar oferece 3 tipos diferentes de ingressos (A, B e C) e, em cada ingresso, há 4 opções de prêmios, o número total de possibilidades de escolha seria:
3 x 4 = 124. Princípio da Adição
Este princípio estabelece que, se uma tarefa pode ser realizada de m maneiras e outra tarefa pode ser realizada de n maneiras, e essas tarefas não podem ocorrer ao mesmo tempo (são mutuamente exclusivas), o número total de maneiras de realizar uma dessas tarefas é dado por m + n.
Exemplo: Se uma pessoa pode escolher entre 3 cores de camisetas e 4 tamanhos de camisas, e essas escolhas são independentes, então o total de escolhas será:
3 + 4 = 7Aplicação da Análise Combinatória
A Análise Combinatória é amplamente utilizada em várias áreas, incluindo:
- Probabilidade: A análise combinatória é crucial para calcular probabilidades em experimentos aleatórios.
- Criptografia: Na criação de algoritmos de segurança, a análise combinatória é utilizada para calcular o número de combinações possíveis em chaves criptográficas.
- Jogos de azar: A combinação e permutação são utilizadas para calcular as chances de eventos acontecerem.
- Design de experimentos: Em estatística e pesquisa, a análise combinatória ajuda a determinar o número de possíveis configurações experimentais.
Fórmulas Importantes
- Permutação simples:
P(n, n) = n! - Permutação com repetição:
P(n, r) = n^r / r! - Combinação simples:
C(n, r) = n! / (r!(n - r)!) - Combinação com repetição:
C(n + r - 1, r)
Conclusão
A Análise Combinatória é uma ferramenta fundamental no estudo da matemática aplicada, especialmente no campo das probabilidades. Sua importância vai além das ciências exatas, influenciando áreas como a estatística, a computação e até a economia. Ao compreender como calcular o número de diferentes formas de organizar ou selecionar elementos, é possível determinar com precisão as chances de ocorrência de eventos e planejar estratégias mais eficientes, seja em jogos, decisões financeiras ou experimentos científicos. O domínio da Análise Combinatória permite uma abordagem lógica e organizada diante de problemas que envolvem múltiplas opções ou resultados possíveis.